❤️‍🔥Time Series Model Forecasting

Applying deep learning or machine learning models to time series data is relatively straightforward. However, there are specialized models and tools specifically designed for time series forecasting. Unfortunately, online tutorials often provide incomplete or even misleading guidance, and the promotion of these tools is uncommon. To address this, Lady H. decided to showcase the capability of methods dedicated to time series analysis.

Statistical Time Series Forecasting - (S)ARIMA

When it comes to time series forecasting, "ARIMA" is a popular method people often talk about, especially during data science interviews. But how many interviewees and even interviewers really used ARIMA in the work, and used well?

Many online tutorials can be misleading, either by omitting crucial information or including unnecessarily complex details. Moreover, they often rely on Air Passenger data as an example, which is too simplistic to reflect real-world challenges. In reality, the performance of a time series forecasting method can vary significantly depending on the dataset.

To address this, Lady H. decided to share the ARIMA process she frequently uses, which has proven to be reliable across various time series problems. The following experiments will use daily sales data as the input:

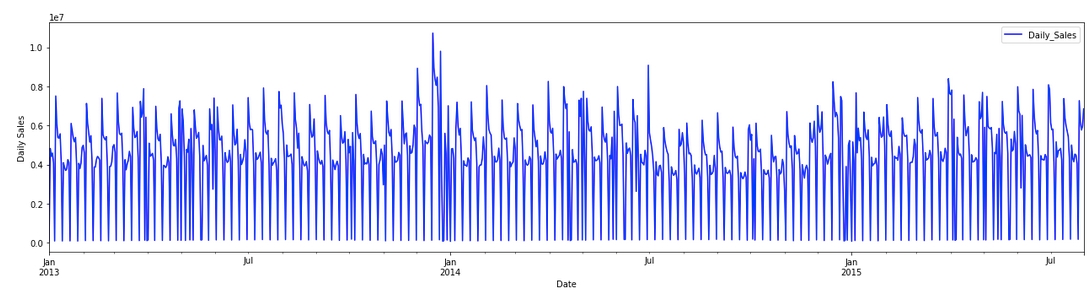
Step 1: Data Exploration

Before applying ARIMA, we can plot ACF and PACF of the data first.

• ACF: It is the autocorrelation plot.

  • Autocorrelation reflects the degree of linear dependency between ith and (i+g)th (g is the lag) time series. Autocorrelation is a value between [-1, 1]. A positive autocorrelation suggests that the values tend to move in the same direction, a negative autocorrelation implies they move in opposite directions, and a value close to 0 indicates minimal or no temporal dependency.

  • In an ACF plot, each vertical bar represents the degree of linear dependency between the ith time point and the (i+g)th time point, referred to as 'autocorrelation.' Given a confidence level (such as 95%), any autocorrelation value outside the confidence interval (indicated by the threshold lines) is considered significant.

• PACF: It is the partial autocorrelation plot. In ACF, the autocorrelation between ith time series and (i+g)th time series can be affected by (i+1)th, (i+2)th, ..., (i+g-1)th time series too, so PACF removes the influence from these intermediate time series and only checks the autocorrelation between ith and (i+g)th time series.

  • Lag0 always has autocorrelation as 1.

Here're the ACF and PACF plots for our daily sales data:

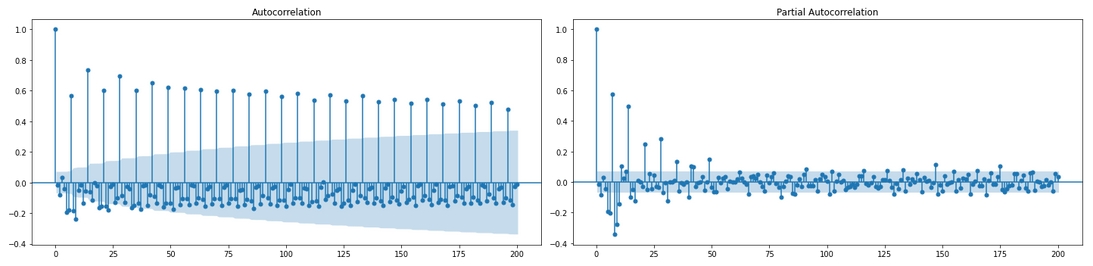
🌻 Check how to plot ACF & PACF >>

Step 2: Estimate ARIMA Parameters

The main reason of checking ACF and PACF plots is to help estimate the parameters of ARIMA.

• ARIMA(p, d, q)

  • p is the order of AR (auto regression) model. AR model makes the prediction based on prior time values, therefore to decide p, we often check PACF to find which lag indicates significant partial auto correlation, and use that lag value as the value of p.

  • q is the order of MA (moving average) model. MA model uses the autocorrelation between residuals to forecast values. We often check ACF to find the value of q.

  • d is the order of differencing needed to convert the time series to stationary.

Thumb rules for choose ARIMA parameter values:

• If ACF is exponentially decreasing or forming a sine-wave, and PACF has significant autocorrelation, then use p

• If ACF has significant autocorrelation and PACF has exponential decay or sine-wave pattern, then use q

• If both ACF, PACF are showing sine-waves, then use both p, q

Let's manually assign ARIMA parameters first. Although ACF and PACF are more complex than the thumb rules situations, we can start with using p. Meanwhile, when checking PACF, there are several lags showing significant autocorrelation. Lady H. tried p between 7 and 10 and found p=7 got better AIC, BIC performance. The detail is shown as below:

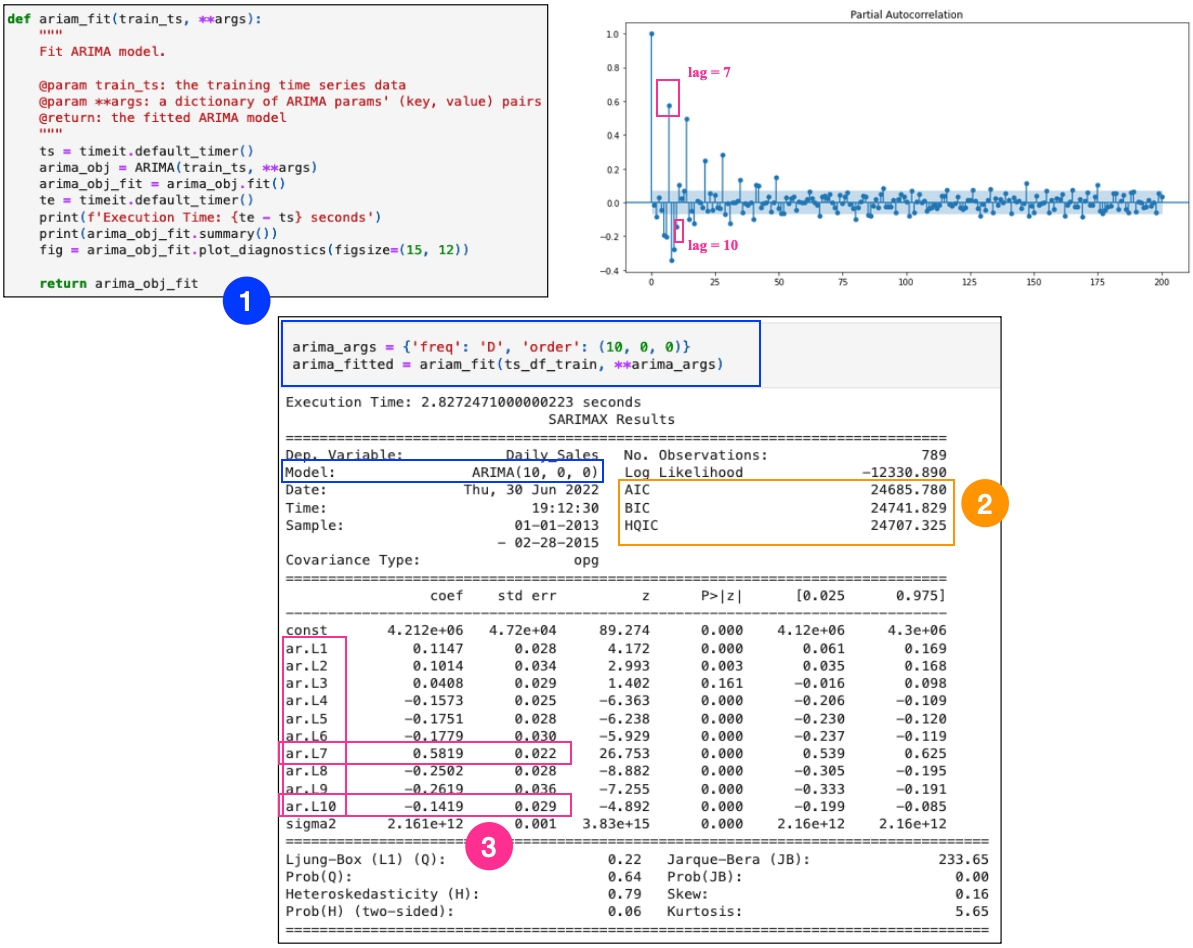
1. Section 1 is showing the code of fitting ARIMA with manually chosen parameters

2. Section 2 is showing the training performance using AIC, BIC and HQIC

3. Section 3 indicates choosing p=7 might get a better performance than using p=10, as PACF shows the highest autocorrelation appears at lag 7 and the fitted ARIMA model shows the highest absolute coefficient and the lowest standard error

The comparision between forecatsed values and the real testing data is shown below, there is not much overlap between the green curve and the orange curve. We are using both MAPE (mean absolute percentage error) and R2 as the evaluation metrics, getting 4.46 MAPE and 0.11 R2, neither is a satisfying metric. We need to improve.

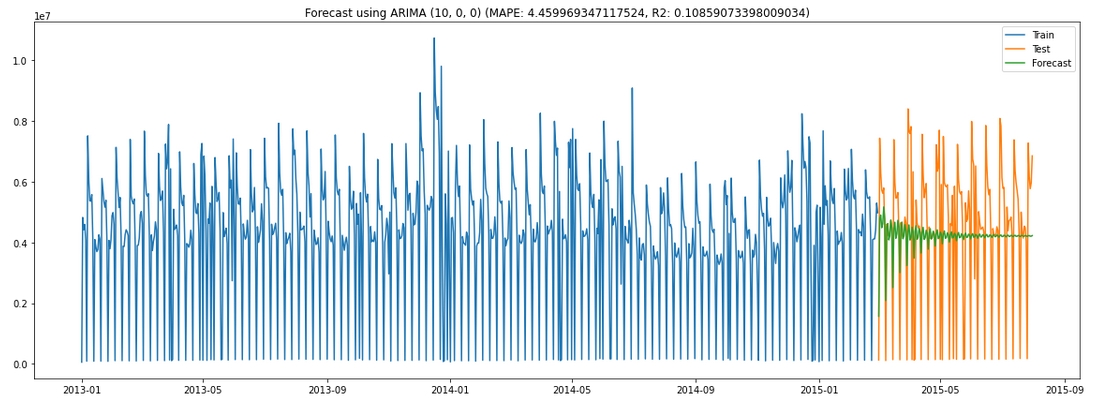
🌻 Check details of Manually Assigned ARIMA >>

Looking at the code, you must have noticed this diagnostic plot from the fitted ARIMA model! How to interpret this plot? Does it help us make further improvement in model performance? 🤔 Let's follow the Chansey Butterflies to learn more! 😉

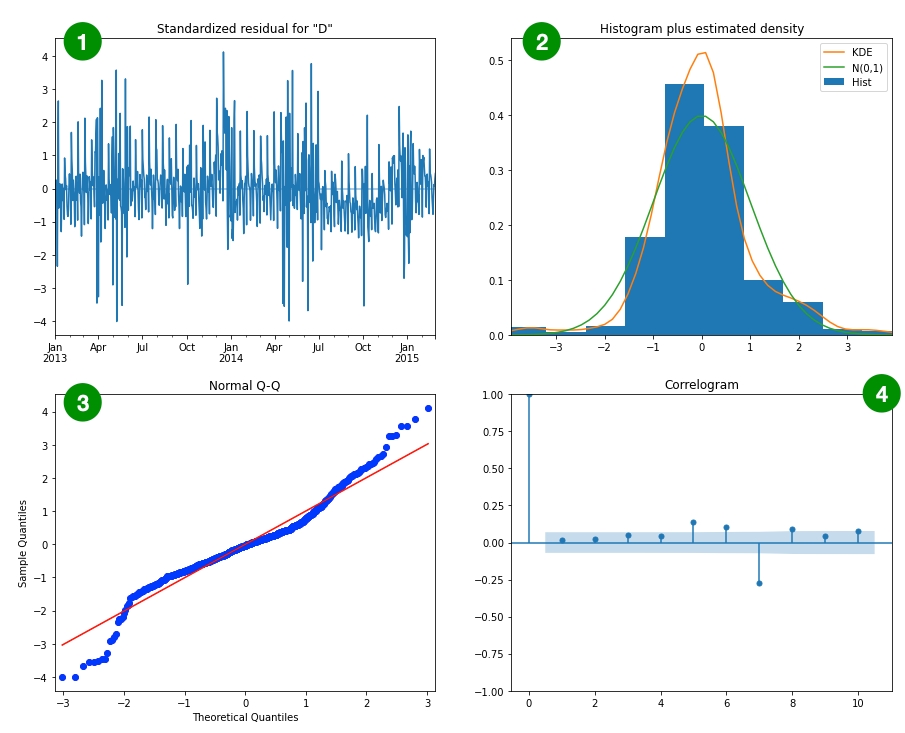
In this ARIMA diagnostic plot:

1. We check the residual plot to see whether it's random, otherwise it means the model needs improvement as it left some time series patterns unexplained.

2. By comparing the orange KDE curve and the green standard normal distribution curve, the larger overlap the 2 curves have, the better model is.

3. Looking at the blue scatter plot and the red line in Q-Q plot, more overlap indicates a better model performance.

4. In correlogram, except lag 0, if we see any significant lag, it means there's seasonality left unexplained by the model. In this case, we are seeing lag 7 has the most significant bar, this also aligns with the 1 week seasonality found in decomposed time series observation and Kats ACF seasonality detector.

To consider seasonality in the model, we can use SARIMA, it adds a seasonality parameter m in the ARIMA model.

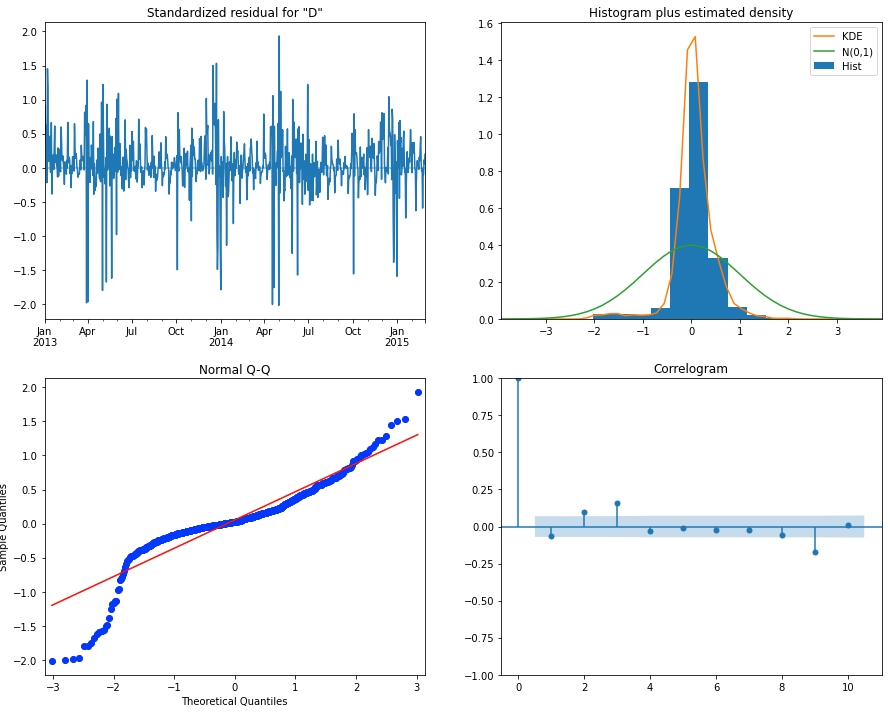
Now let's add m=7 in SARIMA while using (p=10, d=0, q=0) as an example. Note, using p=10 is not conflict with what we just found that p=7 is more ideal, this is just an example, check "Step 3" below for more.

As we can see in the fitted model output below, AIC, BIC, HQIC all became worse:

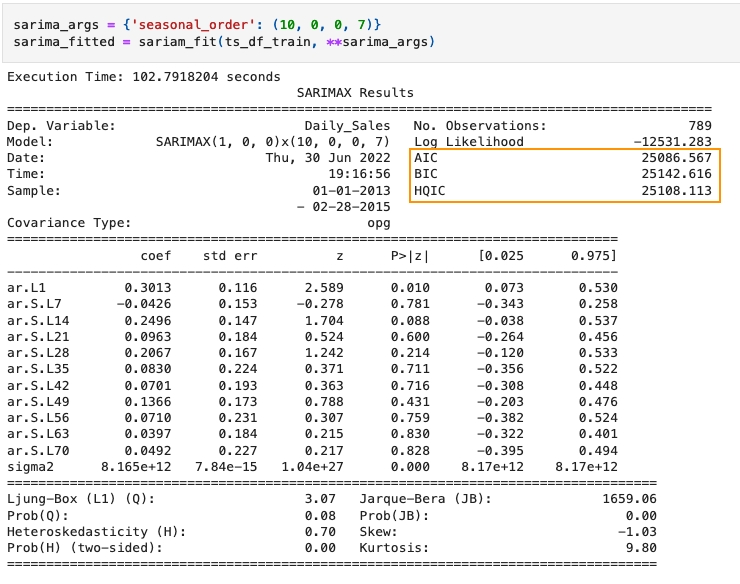
The diagnostic plot also looks worse:

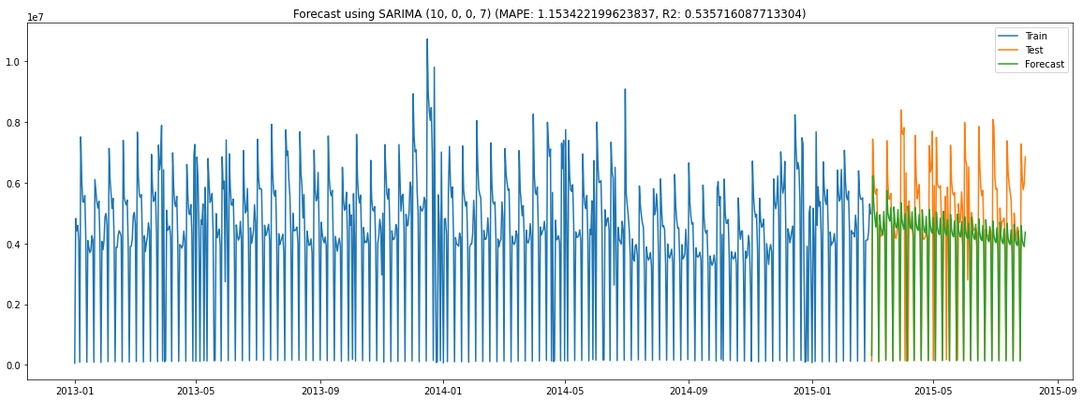
However, we got better forecasting performance as MAPE decreased from 4.46 to 1.15 and R2 increased from 0.11 to 0.54.

🌻 Check details of Manually Assigned SARIMA >>

Seeing such conflicting training and testing performance results, how to assign better parameters became uncertain. Is there a better way to find the parameter values that can further improve model performance?

Step 3: (S)ARIMA Hyperparameter Tuning (HPO)

Lady H. employs grid search to tune the parameters of (S)ARIMA models for improved performance. Typically, the parameter search space is not extensive, so tuning (S)ARIMA models does not require a significant amount of time.

The grid search code is shown below. It iterates through each parameter set and selects the one that achieves the best validation performance, using MAPE as the performance metric. The results align with the findings in Step 2, where p=7 appears to deliver better model performance than p=10.

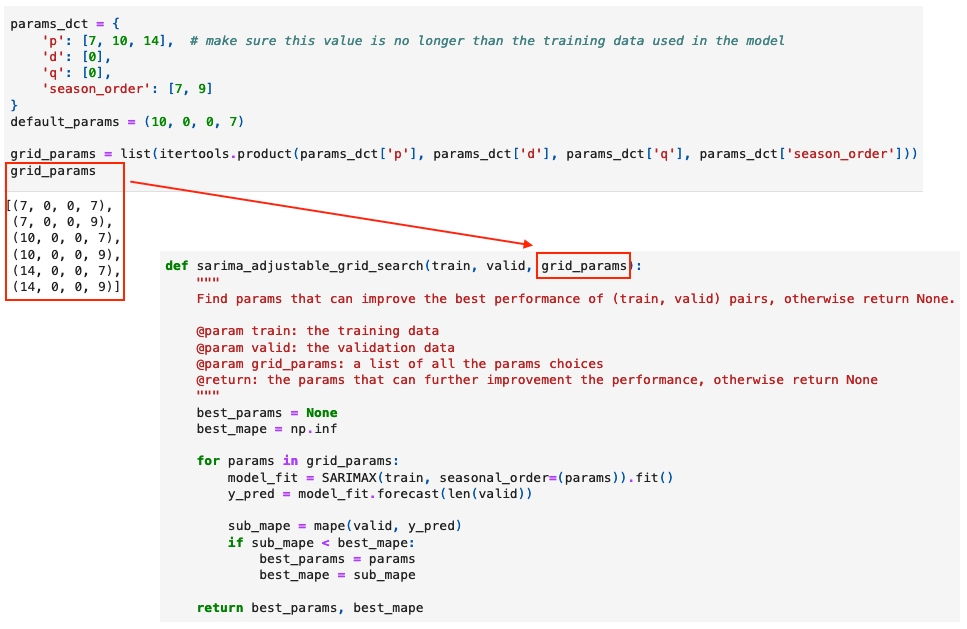
(p=7, d=0, q=0, m=7)is the selected parameter set. The optimized model gets better MAPE but worse R2:

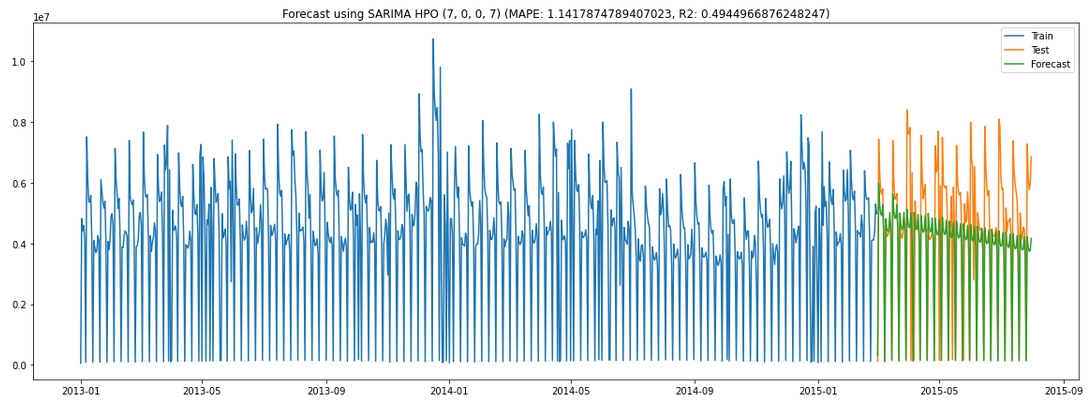
🌻 Check details of HPO SARIMA >>

Here's the forecasting performance comparison between manually assigned ARIMA, manually assigned SARIMA and HPO tuned SARIMA.

You might be wondering why Lady H. doesn't use python built-in auto arima. She did, but got much worse results, especially after adding the seasonality parameter m. Check Lady H.'s failed experiment here.

However, the best result we've seen so far is still not satisfactory. Is there a way to significantly improve both MAPE and R²? Lady H. always has a better solution! Can you guess what's coming next? 😉

Greykite Time Series Forecast

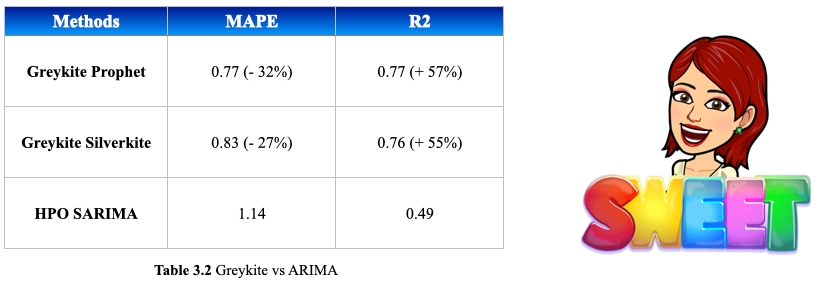
Let’s return to our trusty companion, Greykite. As shown in Table 3.2, compared to the best result from ARIMA, both of Greykite's templates have achieved improvements in both MAPE and R2. How exciting! Now, let’s dive deeper into Greykite forecasting!

Overall Forecasting Process

The overall forecasting process always follow 3 general steps:

1. Config: In this step, you can config settings about data, feature engineering and modeling.

2. Grid Search + CV: In this step, Greykite will tune model parameters with cross validation, using grid search. The returned optimized model will be trained on the whole training data set.

3. Backtest or Forecast: After getting the trained model, if you will predict the labeled testing data, then it's called as "Backtest"; if you need to forecast unlabelled data, then it is called as "Forecast".

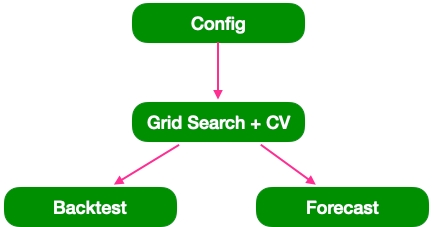
🌻 Check a simplified Greykite forecasting process here >>

This code only shows a baseline model, in order to get a satisfying model performance we need to add more customized configuration. To do the customization, Greykite provides 2 templates: Silverkite and Prophet. Silverkite is a home made algorithm by Greykite (LinkedIn) while Prophet is a forecasting algorithm made by Facebook (a.k.a Meta). Time to look into each template for more details!

Template Silverkite

Silverkite's architecture includes various elements, such as creating features and model configuration, and all these elements can be specified through Greykite config, in a simple way.

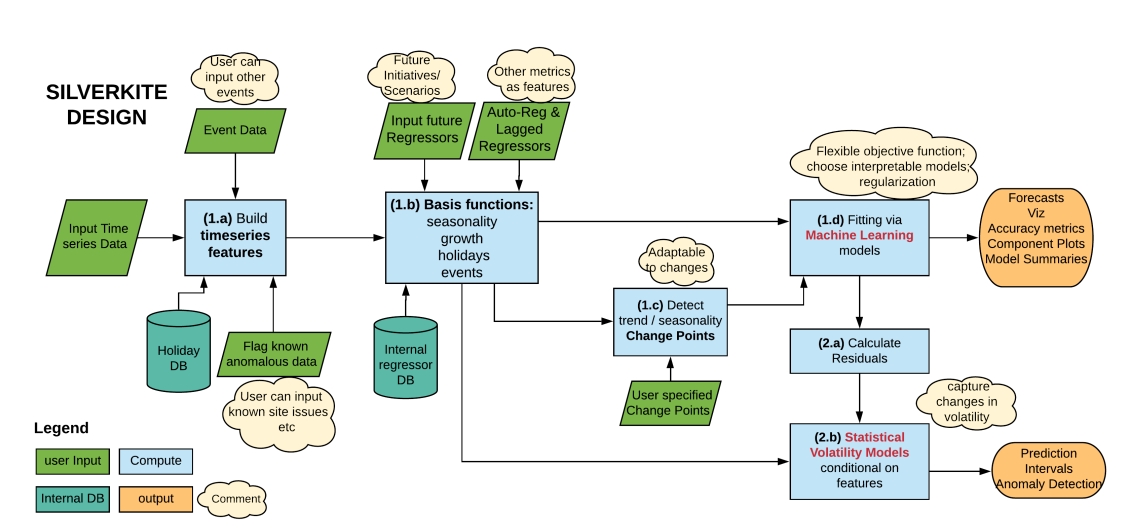
Config

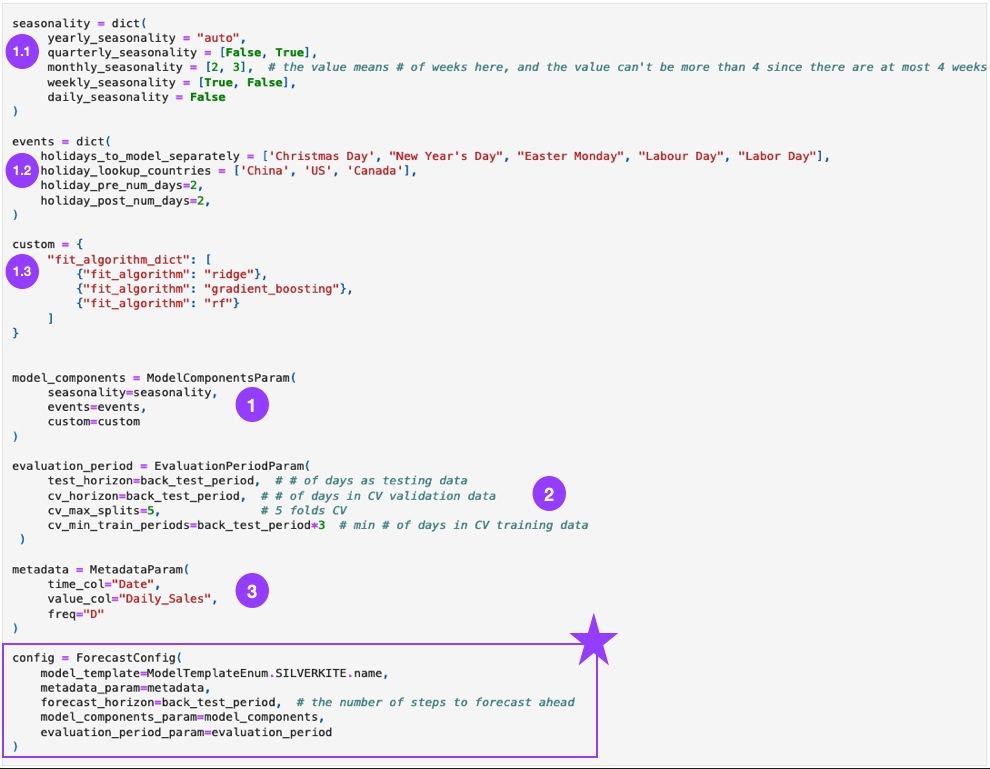
How does Greykite config work? Take a look at the following code:

1. ModelComponentsParam is where you can config feature generation and model settings.

   1. seasonality allows you to specify seasonality features.

   2. events is where to specify special events features. holidays_to_model_separately is to tell Silverkite to use specified holidays independently, and the rest of the holidays will be used together as 1 event.

   3. custom is where to config models' settings.

1. EvaluationPeriodParam contains settings for backtesting and cross validation.

2. MetadataParam is where to describe your time series data input.

As shown below, to finish all the configuration, you only need to put all these settings in ForecastConfig:

In Lady H.'s opinion, the real selling point of Silverkite is its feature engineering, such as seasonality features, events features, etc. Models used in Silverkite are classical machine learning algorithms, such as linear regression, random forest, gradient boosting, etc. Take a look at Silverkite source code here, there's nothing special in model fitting, but the generated features often make a difference.

After configuration, we can initialize a forecaster instance as simple as the code below:

🌻 Check detailed code of using Silverkite template >>

Grid Search with Cross Validation

After configuration, now we are ready to train and select the optimal model. Greykite uses grid search with cross validation to find an optimal forecating solution:

The cross validation output will show evaluation metrics values for each parameter set.

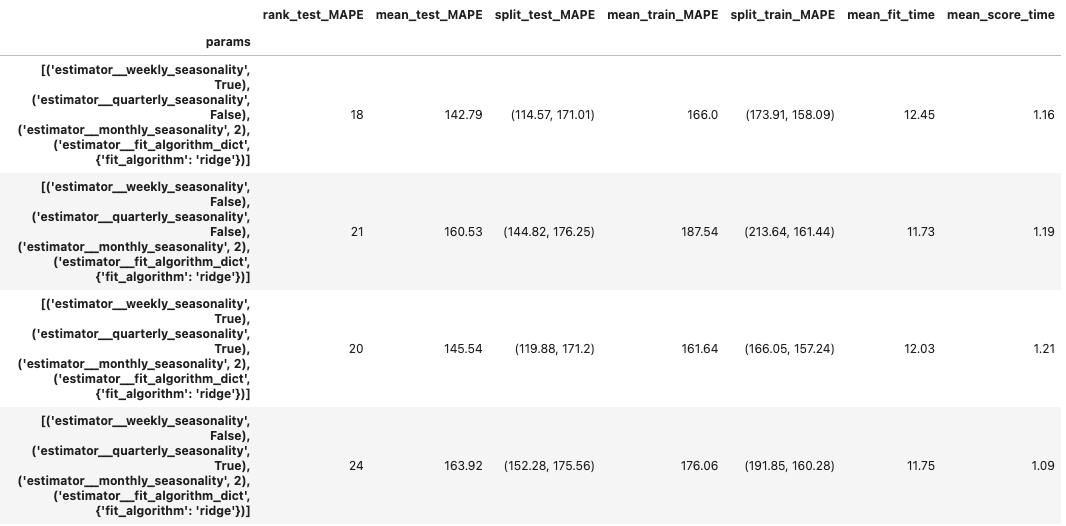
🌻 Check detailed code of using Silverkite template >>

Backtest

With the optimized model, now we can do backtest and forecast. Here's the backtest code:

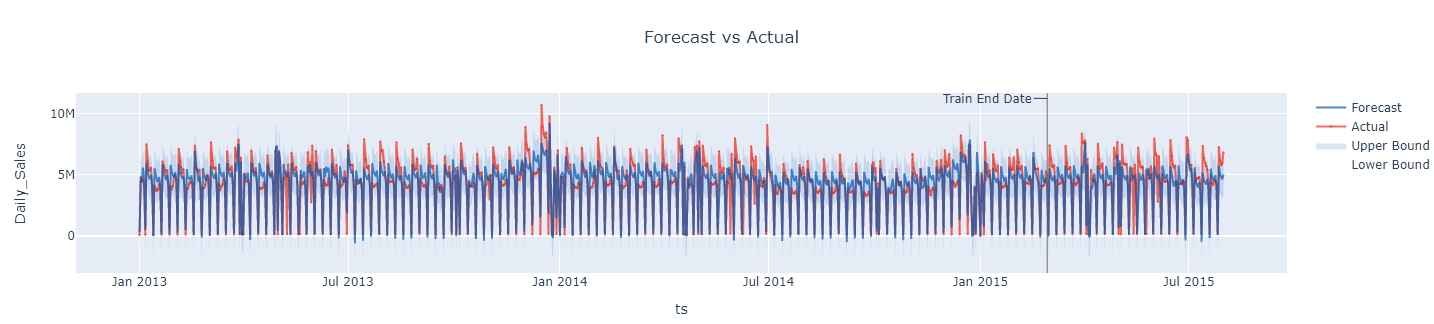
As menitoned before, in Greykite, "backtest" is to predict a set of labeled testing data, that's why when configuring EvaluationPeriodParam we need to specify the testing data period through test_horizon. In this backtest output plot, the testing data starts from "Train End Date", and we can see the comparison between the forecasted value (blue curve) versus the actual value (orange curve).

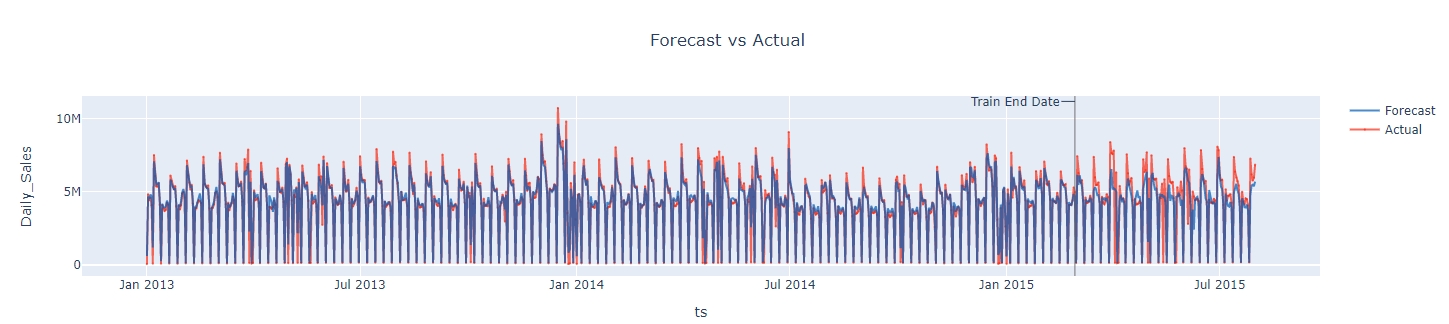
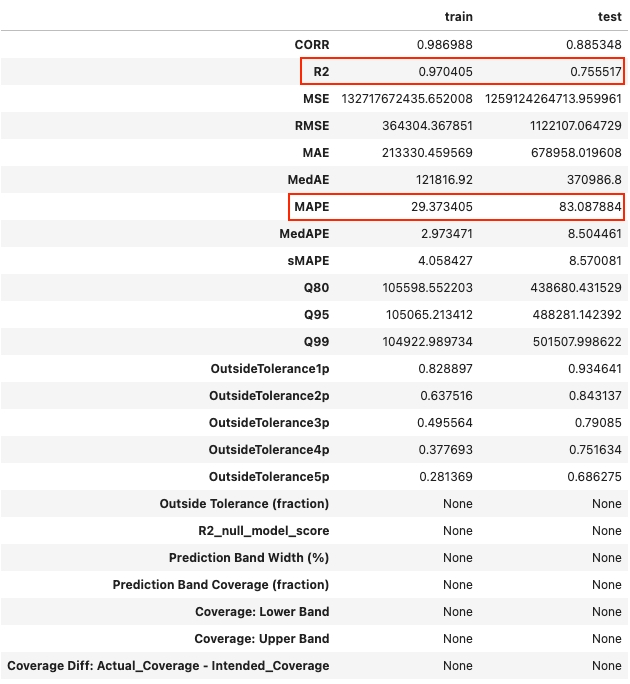
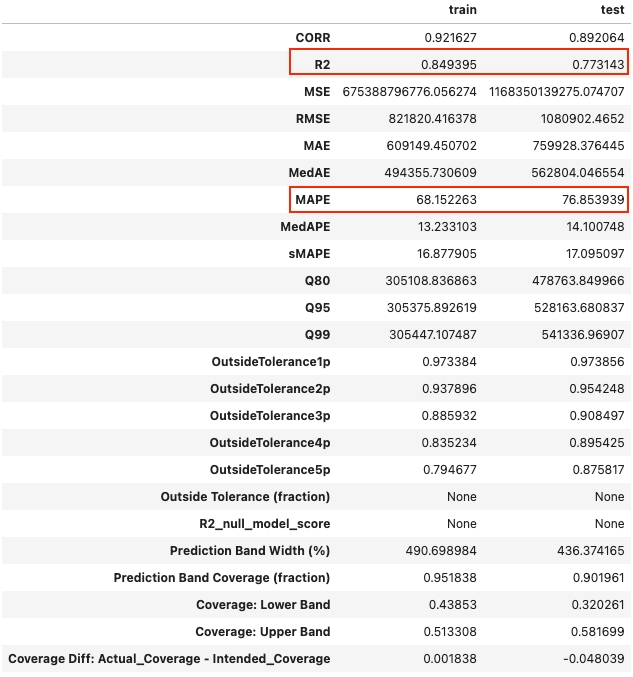
Besides the plot, Greykite also output a list of evaluation metrics during the training and testing stage. To compare with ARIMA best results, we only look at R2 and MAPE here. Note that, we need to divide Greykite's MAPE by 100 in order to compare with sklearn MAPE.

Here we can see, comparing with the best ARIMA results we got, Silverkite template improved MAPE from 1.14 to 0.83 (27% decrease) and improved R2 from 0.49 to 0.76 (55% increase).

🌻 Check detailed code of using Silverkite template >>

Forecast

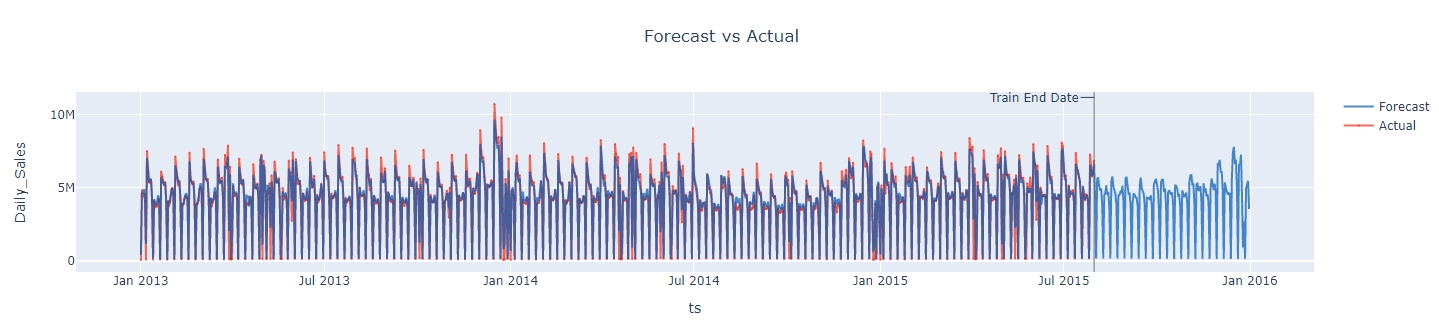
Comparing with backtest, forecasting in Greykite is to predict the future unlabeled data. The code is as simple as the backtesting code:

The forecasted result is shown as below:

Model Summary

Besides the prediction results, Gryekite also provides a model summary. As the generated features play a core part in Greykite forecasting, the model summary mainly shows the feature contributions to the model. For example, here's part of the model summary from the experiment above. It's showing random forest is the selected model, also outputs the features used in the model as well as their feature importance:

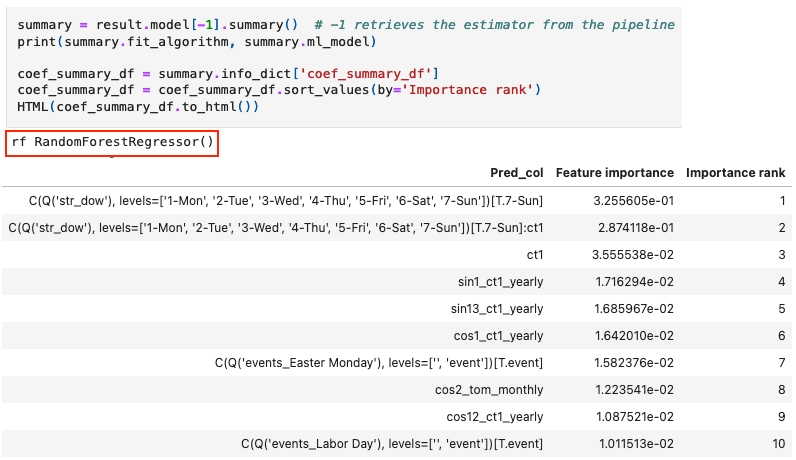
In this sample summary, we can find different types of features:

• C(Q('str_dow'), levels=['1-Mon', '2-Tue', '3-Wed', '4-Thu', '5-Fri', '6-Sat', '7-Sun'])[T.7-Sun] is a type of seasonality feature, it's using day of week ("dow") as the feature.

• ct1 is a linear growth feature, it counts how long has passed since the first day of training data (in terms of years). To learn more details, check "Growth" here.

• Features start with "sin" and "cos" are fourier features, these features treat the time series as a wave, trying to capture the amplitude and frequency from it.

• There are also events features such as "Easter Monday", "Labor Day", etc.

• Features contain the colon : are feature interactions.

Through Greykite model summary, we can also check all the feature interactions used in the model:

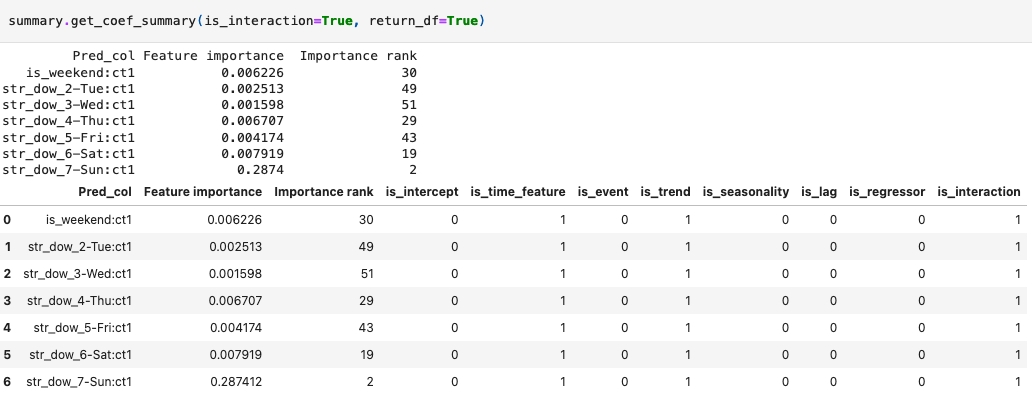
🌻 Check detailed code of using Silverkite template >>

We have now explored forecasting with the Silverkite template. As shown in Table 3.2, the Prophet template delivers even better performance. How does applying the Prophet template differ? Let’s move forward and find out!

Template Prophet

Prophet doesn't have a cool photo like Silverkite's design architecture, so Lady H. decided to make one! 👇

See this formula? All the secrets of Prophet are hidden here! 👆

Instead of considering the data's temporal dependency like (S)ARIMA, Prophet model frames the forecasting problem as a curve-fitting exercise by using a trend function g(t), a seasonality function s(t), a holiday function h(t) and the error term εt. The benefit of Prophet model is the flexibility that users can adjust model parameters with different assumptions about the trend, the seasonality or the holidays. Prophet is a convenient time series forecasting tool with insightful visualization, to learn more details check Prophet paper. Now let's see how can we use Prophet template in Greykite!

Config

The difference between Prophet and Silverkite templates, mainly lies in the configuration settings.

• seasonality_mode is a unique parameter in Prophet template. It supports "additive" or "multiplilicative" modes. Mode "additive" is used when you assume the seasonality is constant over the time, and Prophet will add seasonality to trend in the formula. Mode "multiplicative" is used when you assume the seasonality is time varying, and Prophet will multiply the seasonality with the trend.

• add_seasonality_dict is also Prophet unique. You can define different cycles for seasonality such as "monthly", "quarterly", etc. In each cycle, you can define the period and fourier order. Fourier allows faster fitting in changing seasonality cycles, but could also lead to overfitting. N Fourier terms corresponds to 2N variables used for modeling the cycle.

• In events, with Prophet you don't need holidays_to_model_separately to specify any event independently. Prophet will handle each event listed in holiday_lookup_countries for you. Besides, in Prophet template, holiday_pre_num_days and holiday_post_num_days have to be list format. While in Silverkite, these 2 variables can be either integer or list format.

• Configuration of model_components, evaluation_period and metadata can be the same as Silverkite, since they are not dependent on the algorithm of Silverkite or Prophet, but more dependent on Greykite framework. Also note, in Prophet template, we no longer need custom to specify which algorithms to use, since Prophet has its built-in forecasting algorithm.

• Finally, we put all the config parameters in ForecastConfig. Comparing with Silverkite, Prophet has coverage parameter to generate the lower and upper bounds for forecasted value. The idea is the same as the confidence interval of model forecasting that, instead of getting a specific forecasting value, you can get a value range of the forecast.

🌻 Check detailed code of using Prophet template >>

Model Output

The code of applying grid search with cross validation, backtest and forecast are the same as Silverkite template. We can look at the output directly here.

The grid search in Prophet template has less parameters to tune, so we got a shorter output:

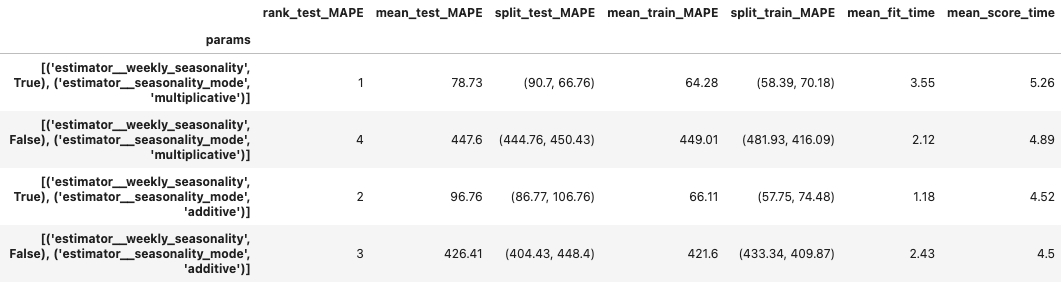
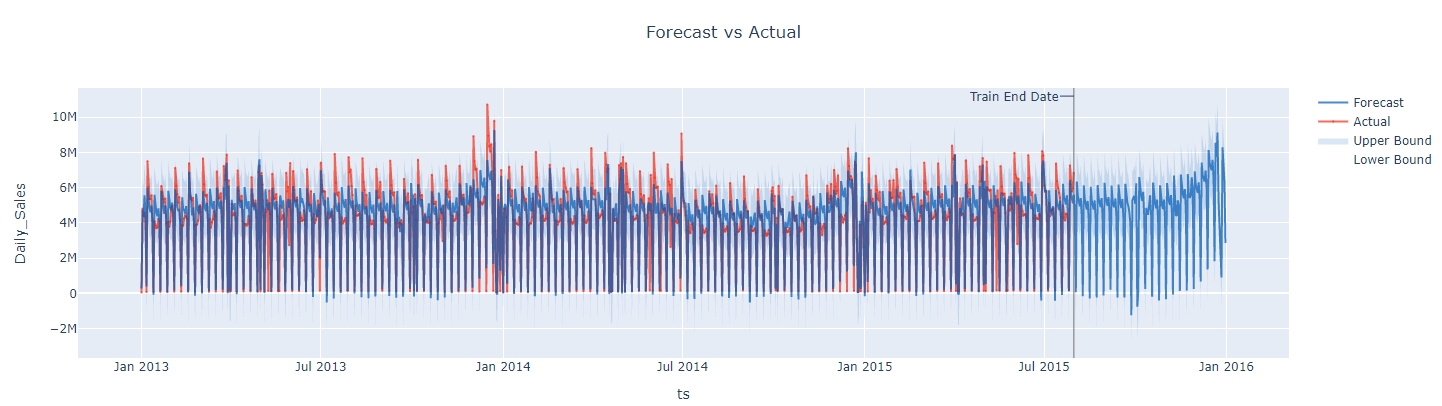
Backtest ouptut plot:

Looking at the R2 and MAPE backtest results, comparing with the best ARIMA results we got, Silverkite template improved MAPE from 1.14 to 0.77 (32% decrease) and improved R2 from 0.49 to 0.77 (57% increase).

Finally, this is the forecasting plot:

🌻 Check detailed code of using Prophet template >>

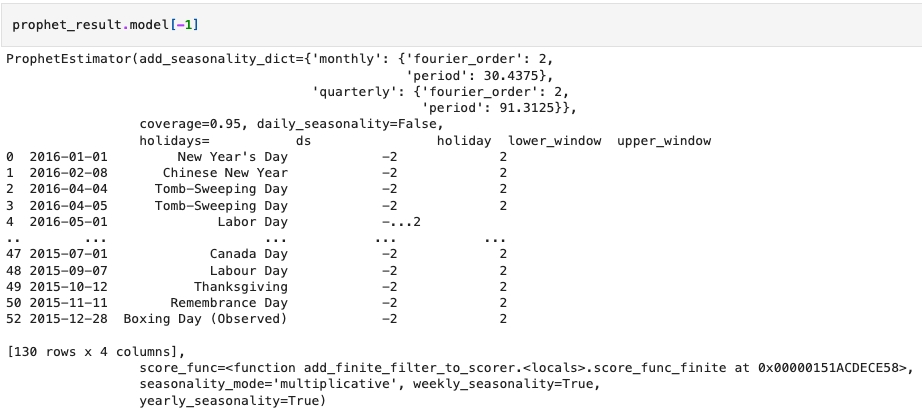
Model Summary

Although using Prophet template, we got better model performance in both MAPE and R2, its model summary is a shame. Look, this is all you can get:

🌻 Check detailed code of using Prophet template >>

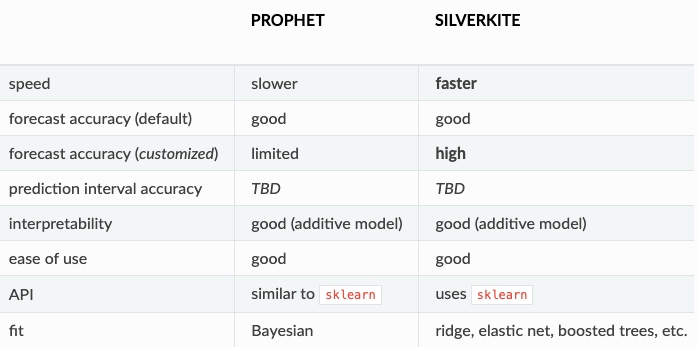
Silverkite vs Prophet

In the experiments, Prophet template demonstrated slightly better performance with less parameters to tune.

At the same time, Greykite provided a comparison between these 2 templates (reference):

Greykite also provided the customization comparison:

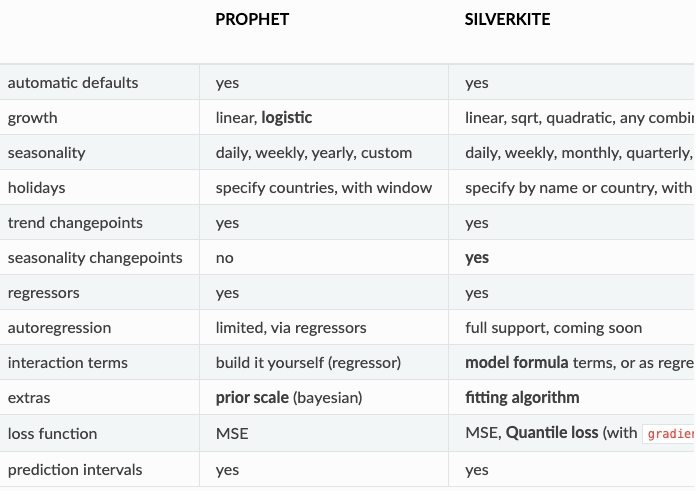
However, do you think Greykite would claim on its homepage that Prophet (developed by Meta) is better than Silverkite (developed by LinkedIn)? 😁 Deciding which one to use still depends on your own judgment and experience. Overall, Greykite seems to be a solid forecasting tool. The only drawback is that Lady H. couldn’t find a way to save the trained model for future reuse.