❤️‍🔥Time Series Data Exploration

Unlike traditional datasets, time series data contains hidden temporal patterns, offering a unique and engaging experience during data exploration. Let’s explore some popular and practical methods!

Explore Univariate Time Series

About the Data

Our perfume sales data is a classic example of time series data. Specifically, it is a univariate time series, meaning there is only one time-dependent variable (in this case, Daily_Sales). Take a look at the example below:

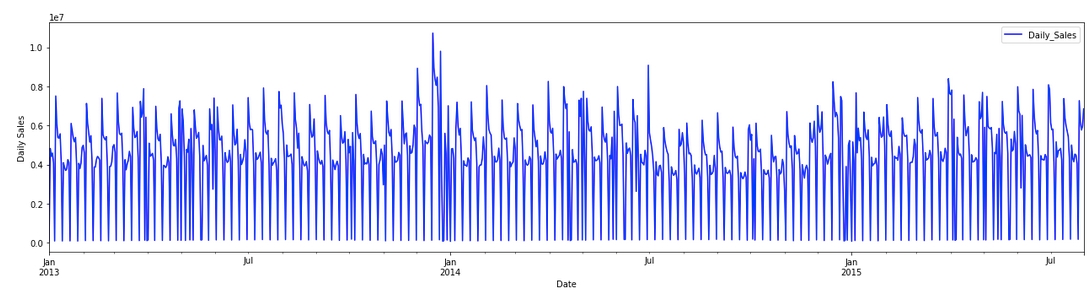
Here’s the sales plot. As you can see, the data shows a clear, recurring pattern of ups and downs:

🌻 To get sales time series data >>

Time Series Components

A time series sequence consists of several key components:

• Trend: Represents the overall direction of the time series, such as upward, downward, or stable with no trend.

• Seasonality: Refers to consistent, repetitive fluctuations occurring at regular intervals, often linked to the calendar.

• Cycle: Similar to seasonality but with irregular frequencies. Cycles are less frequent and may span longer periods than seasonal changes. Unlike seasonality, cycles are not time-dependent and are typically influenced by external factors.

• Residuals: The random error component, which does not systematically depend on time. Residuals arise from missing information or random noise and are irreducible.

To analyze a time series sequence, we often begin with decomposition, a process that separates the sequence into its trend, seasonality, and residual components. There are two types of decomposition methods:

• Additive Method:

  • Formula: Y[t] = T[t] + S[t] + E[t]

  • Assumes the time series value at time t is the sum of the trend (T), seasonality (S), and residuals (E) at time t. Typically used when the trend component is time-dependent but seasonality remains constant in amplitude and frequency over time.

• Multiplicative Method:

  • Formula: Y[t] = T[t] * S[t] * E[t]

  • Generally applied when the seasonality varies in amplitude over time.

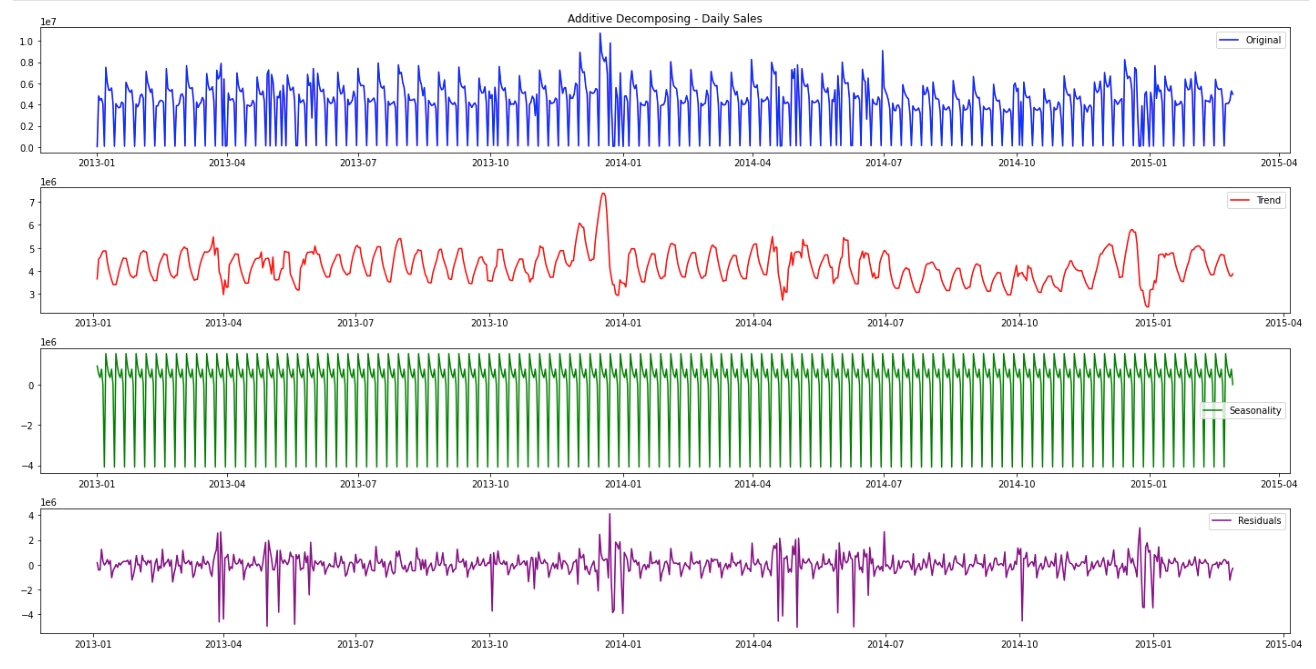
Let's look at the decomposition of our sales data. This is the additive decomposition:

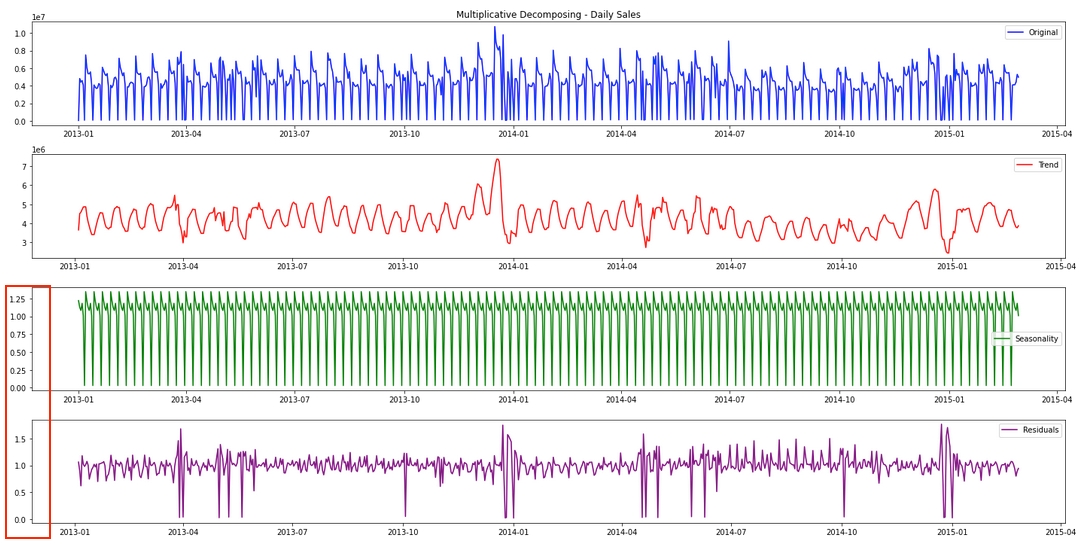
This is the result of the multiplicative decomposition. At first glance, it looks almost identical to the output from the additive method, right? However, as highlighted below, the scale of the data in the seasonality and residual components is noticeably different.

🌻 Check detailed code in Time Series Decomposition >>

Observations:

• The seasonality repeats almost every 7.5 days, that's around 1 week.

• The seasonality is constant.

• The residuals tend to have larger fluctuations between April and July, or at the beginning of a new year or at the beginning of October, this insight might be useful in later feature engineering for model forecasting.

Stationary Analysis on Univariate Time Series

In the field of time series analysis, certain statistical methods, such as ARIMA, assume that the data is stationary. Therefore, it is often necessary to transform the data into a stationary form before applying these methods. A time series is considered "stationary" if it has a constant mean and variance over time. In other words, a stationary time series is not influenced by time but exhibits consistent statistical properties throughout."

To determine whether a time series is stationary, Lady H. typically uses three methods together:

1. Plotting the rolling mean and rolling standard deviation: This involves visualizing the rolling mean and standard deviation over time. If they appear constant, it suggests that the time series has a stable mean and variance, making it likely stationary.

• A "rolling" value is calculated using a smaller time window, which is moved along the time series to produce a series of values. This smaller window is referred to as the "rolling window."

• However, visual judgment of constancy can be subjective. To confirm, more rigorous tests like the ADF and KPSS tests should also be applied.

1. Augmented Dickey-Fuller (ADF) Test: This statistical test checks for differencing stationary by focusing on whether the data is stationary after differencing.

2. KPSS Test: This test examines whether the time series is stationary around a deterministic trend (trending stationary).

By combining these methods, a more reliable assessment of stationarity can be made.

Here's the code to do these tests:

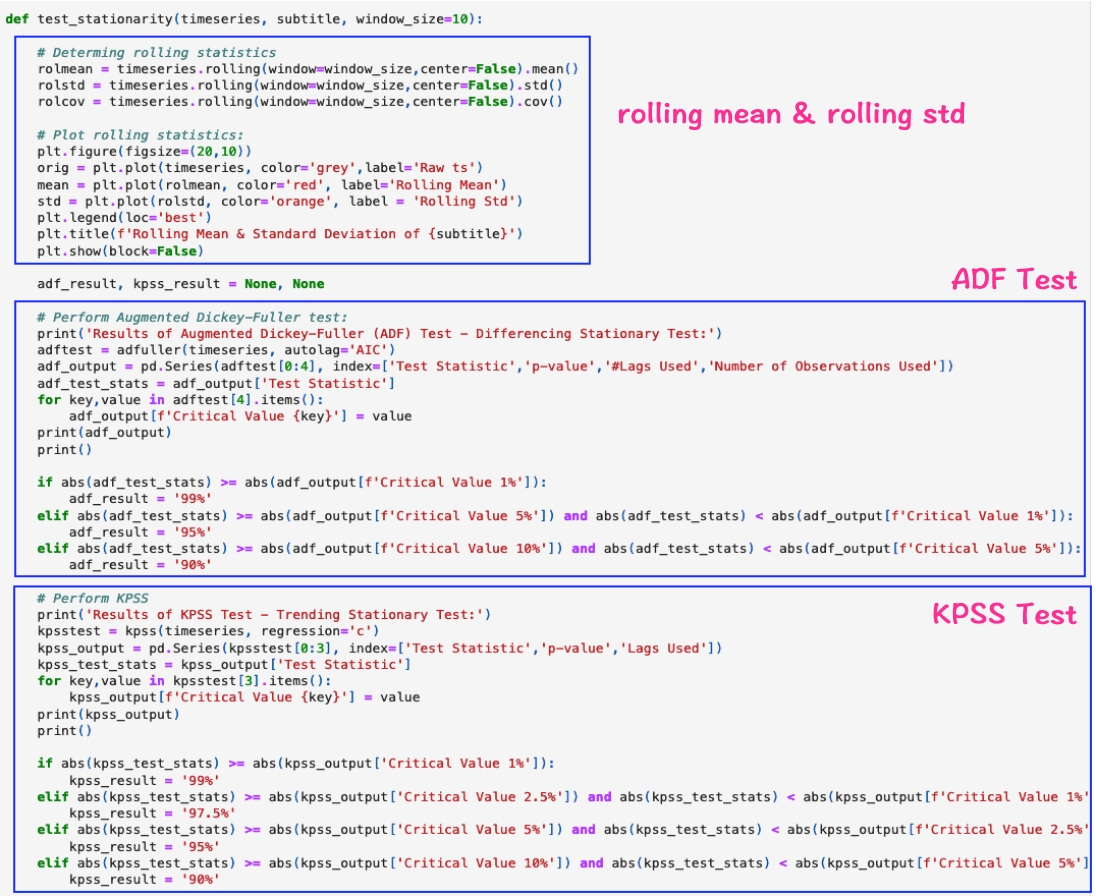
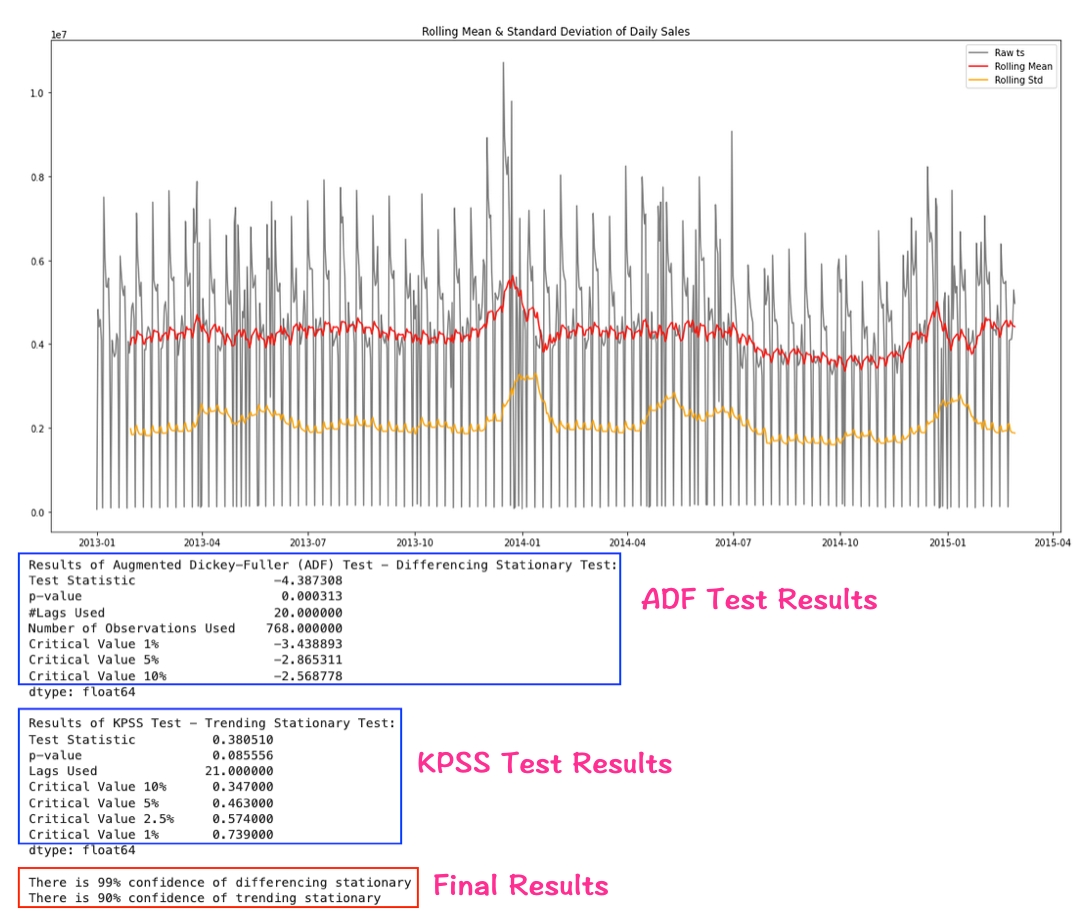
We often start to check the stationary of the original time series. Let's take a look at the stationary analysis on our sales data.

• Looking at the rolling mean and rolling standard deviation, some people might think it looks constant while others won't, this is why the visualization only provides an idea and we need to look into more statistical details.

• To interpret the ADF test results, we compare the "test statistic" to the critical values. A larger absolute value of the "test statistic" indicates a higher likelihood of being stationary. In this case, the absolute "test statistic" is 4.387308, which exceeds the absolute "critical value" at the 1% significance level (3.438893). Therefore, we can conclude with 99% confidence that the time series is differencing stationary.

• Similarly, for the KPSS test, we compare the "test statistic" to the critical values. Here, the absolute "test statistic" is 0.380510, which is greater than the absolute "critical value" at the 10% significance level but smaller than that at the 5% level. This indicates the time series is trending stationary with 90% confidence.

🌻 Check detailed code in Stationary Analysis on Univariate Time Series >>

The above results indicate that our sales data is already stationary, so we don't need to do any extra work. However, there are many real world time series data needs more effort. If you will see the time series is not differencing stationary (failed ADF test), then you can try 1st order differencing on the time series data.

• 1st order differencing = y_i - y_i-1, and the code can be written as:

If ADF test still failed after 1st order differencing, you can try 2nd order differencing.

• 2nd order dofferencing = (y_i - y_i-1) - (y_i-1 - y_i-2) = y_i - 2*y_i-1 + y_i-2, and the code can be written as:

Often times, do the differencing till 2nd or 3rd order is enough, if you still can't get a stationary output, it means differencing is not a preferred method. But what to do then?

Here comes another method, which is to check residuals' stationary, since residuals is supposed to be time independent. If the residuals is stationary, in some applications, we can simply use residuals as the input of those statistical models.

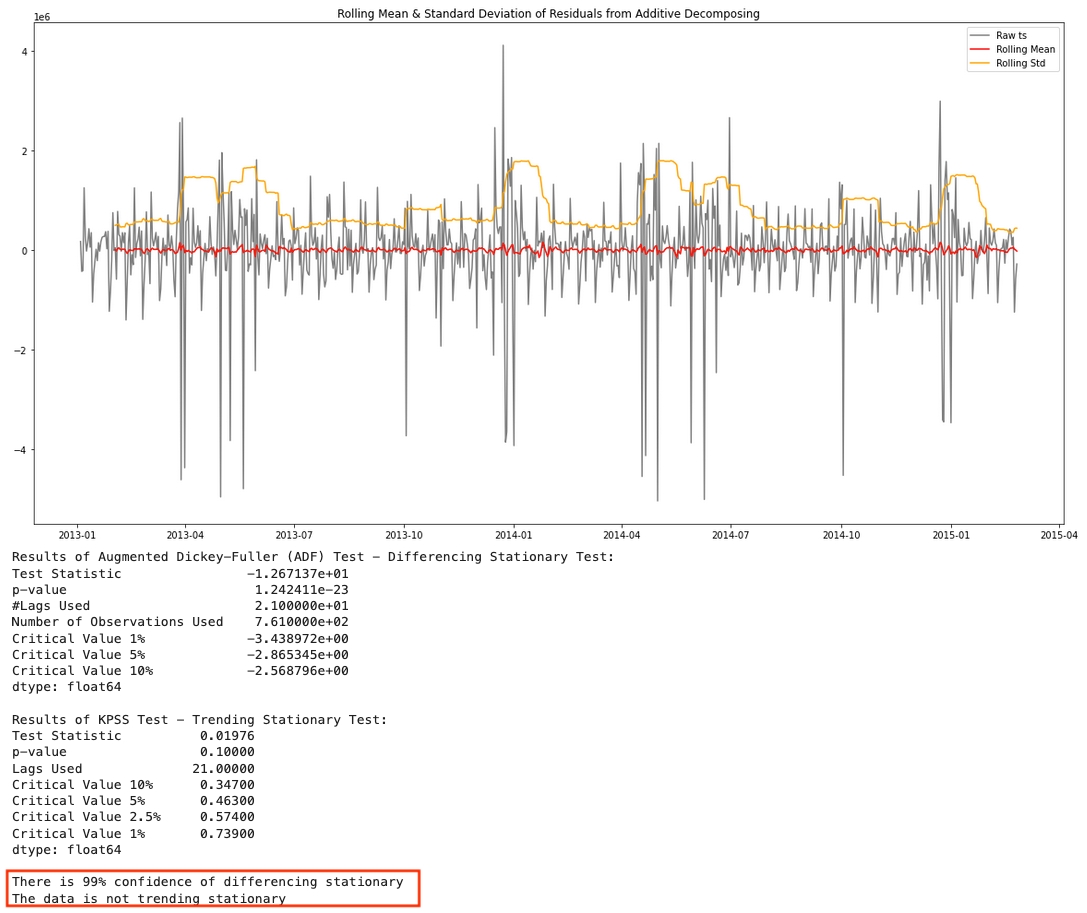
Let's look at the stationary analysis on the additive decomposition residuals first. It appears to be differencing stationary but not trending stationary.

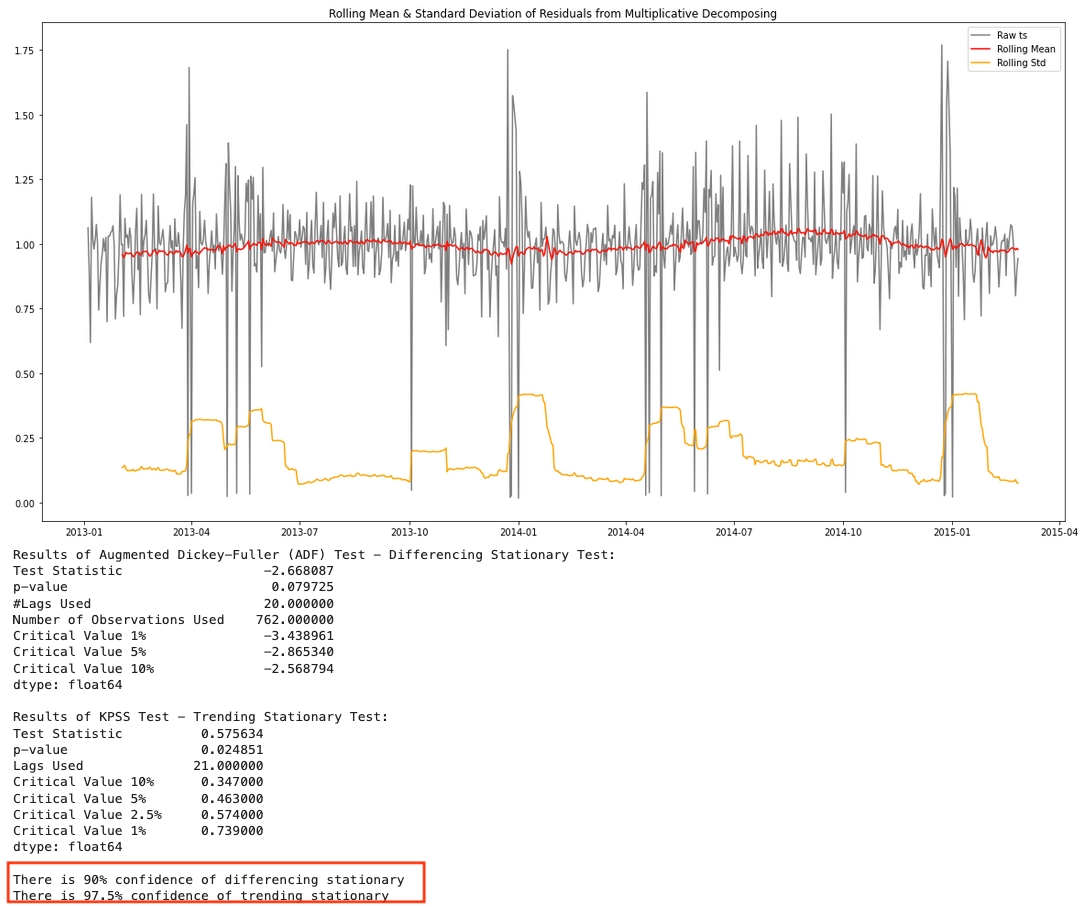
Now let's do stationary analysis on the multiplicative decomposition residuals, it appears to be both differencing stationary and trending stationary.

🌻 Check detailed code in Stationary Analysis >>

Lady H. collected a few more tips to make the data stationary 😉:

• Differencing is often a way to remove trend.

  • Besides 1st, 2nd, 3rd order differencing, you can also try seasonal differencing.

• Log or square root is popular to handle the changing variance.

• Moving average (rolling mean) can smooth the time series by removing random noise.

  • This example includes both moving average and m*n weighted moving average.

    • Moving average only applies rolling() followed by mean() once

    • m*n weighted moving average applies rolling mean on window m and then applies on window n again. m often chooses the periodicity of the seasonal data. This method aims at seasonal smoothing and gives better estimate of the trend.

  • However, moving average can also reduce the variance of the dataset and lead to model overestimation later, be cautious❣️

Forecastability Analysis

The basic idea of "forecastability" is, when a time series has higher chance of having repetitive patterns, then it's more predictable. We use Approximate Entropy or Sample Entropy to measure this forecastability.

• Approximate Entropy measures the likelihood that similar patterns of observations will NOT be followed by additional similar observations. A lower Approximate Entropy indicates a lower likelihood of this occurring, suggesting the time series has more repetitive patterns and is therefore more predictable.

• Sample Entropy is an improved version of Approximate Entropy. It is independent of data length and easier to compute. Unlike Approximate Entropy, which tends to overestimate the regularity of a time series due to "self-matches," Sample Entropy eliminates self-matches, providing a more accurate measure of regularity.

We often use sample entropy rather than approximate entropy in the work.

From previous stationary analysis, we have seen that the original sales data and its multiplicative residuals are both stationary, and in the comparison below, the original time series has lower entropy values and therefore appear to be more forecastable.

Does this mean, when a time series and its residuals are both stationary, the original time series should be more predictable because it didn't remove those repetitive patterns (such as seasonality)? You are very welcome to discuss your opinions here.

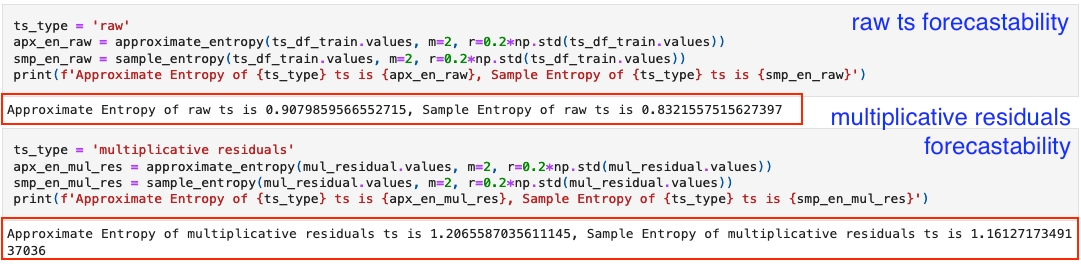
🌻 Check detailed code in Forecastability Analysis

Explore Multivariate Time Series

Comparing with univariate time series, multivariate time series has more than 1 time dependent variables.

About the Data

Our garden features a massive green warehouse housing hundreds of smaller greenhouses, each dedicated to cultivating sprouts of various species. To ensure a healthy growing environment, every greenhouse is continuously monitored. One key metric we track is "occupancy". By analyzing factors such as temperature, humidity, light, CO₂ levels, and humidity ratios, we can accurately predict whether a greenhouse has enough space to accommodate new sprouts.

Here's the data sample of a greenhouse's data:

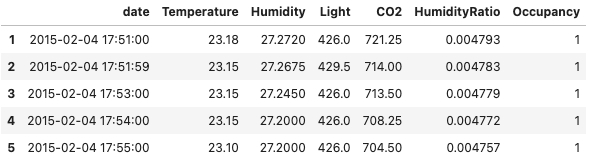
The 5 variables are recorded nearly every minute. When we examine each variable over time, they display distinct trends and seasonal patterns, except for humidity and humidity ratio, which exhibit almost identical curve shapes.

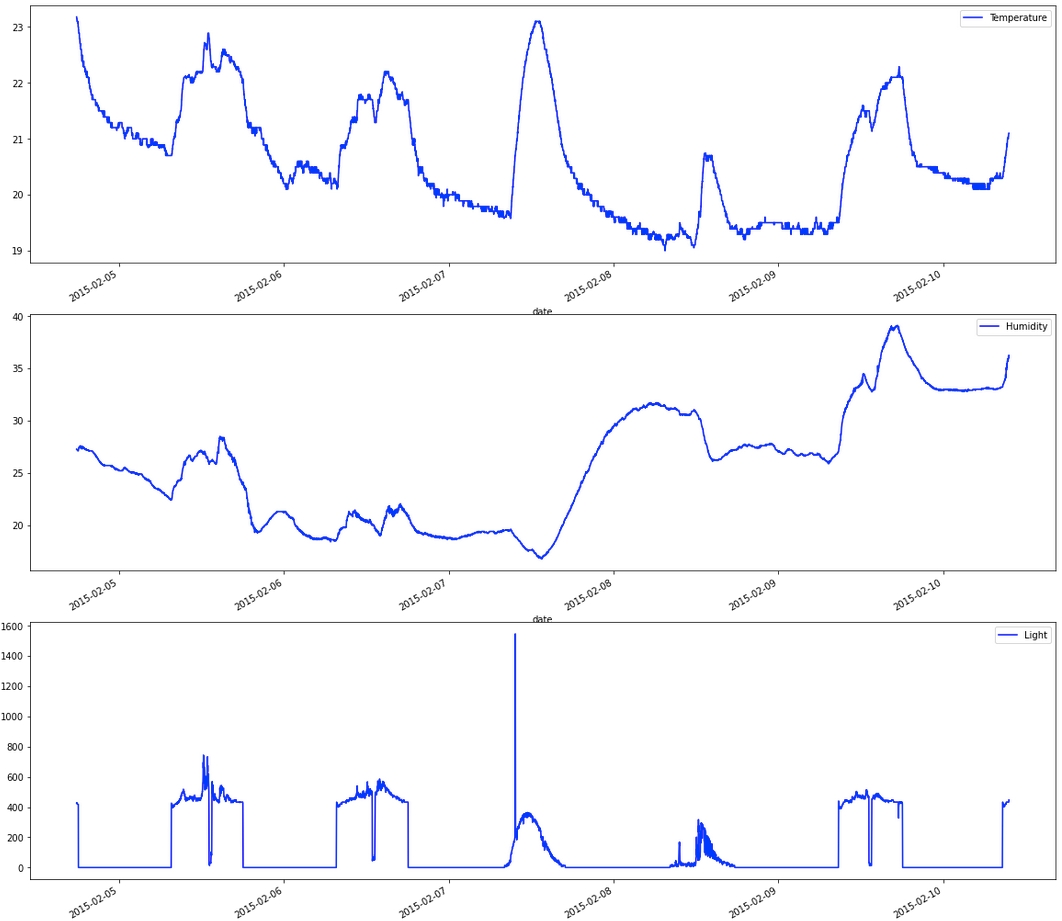
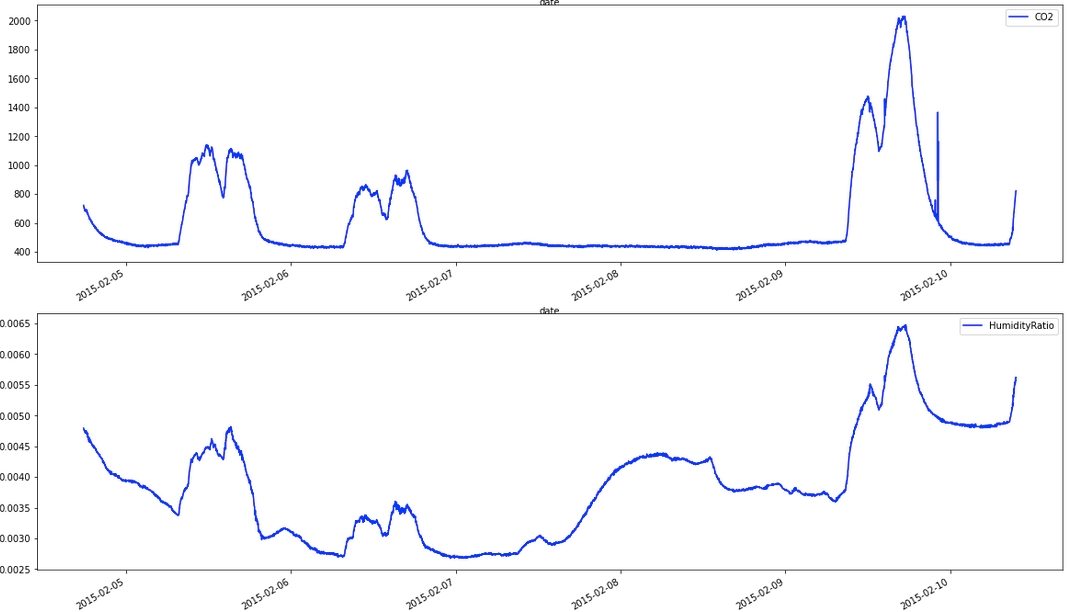
Meanwhile, below is the plot of the forecasting target, "Occupancy":

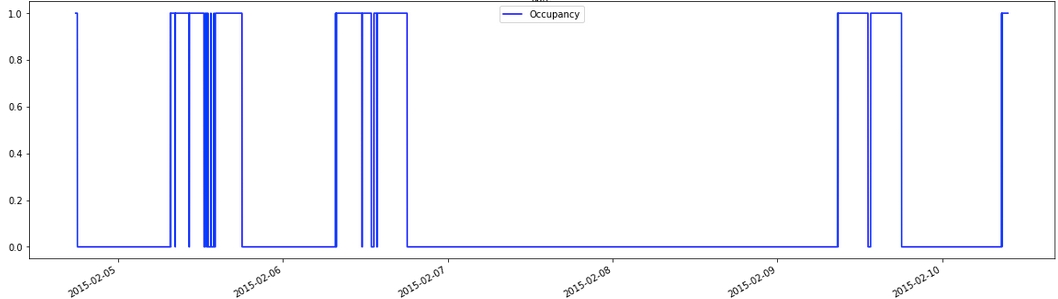
🌻 To get multivariate time series data >>

Stationary Analysis on Multivariate Analysis

Some statistical models require each variable in a multivariate time series to be stationary.

If we do a stationary analysis on our green houses' data, we can see neither humidity nor humidity ratio is differencing stationary.

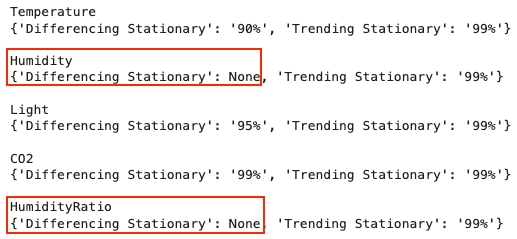
If we apply 1st order differencing here, both humidity and humidity ratio will become stationary.

🌻 Check detailed code of Stationary Analysis on Multivariate Time Series >>

Comparing with univariate time series, there is more fun we can explore in multivariate time series, such as exploring the relationships between its variables. Let's go to see more! 😉

Cointegration Test

As we know, a multivariate time series consists of multiple time-dependent variables, each forming its own time series. The cointegration test evaluates significant relationships between two or more time series. Meanwhile, cointegration is a prerequisite for certain models, such as Vector Autoregression (VAR), it is essential to perform a cointegration test before applying these models.

Then what does "cointegration" mean, statistically? We need to understand what is the "order of integration (d)" first.

When two or more time series have a linear combination with an order of integration (d) lower than that of each individual series, the series are said to be cointegrated.

We often use Johansen test as cointegration test. It's based on the estimation of expected maximization through maximum likelihood, under various assumptions about the trend and intercepting parameters of the data. Python statsmodels provides built-in coint_johansen.

Note: The input data here is already converted to stationary from previous stationary analysis step!

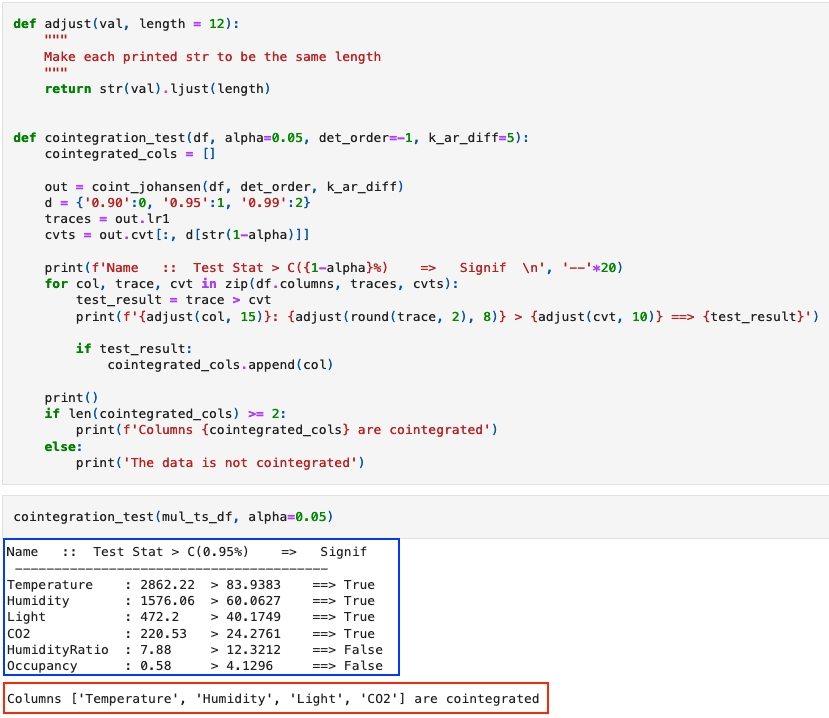
As the output shows, there is cointegration in the data, and we can apply VAR on it later.

🌻 Check detailed code for Cointegration Test >>

Granger Causality

When exploring the relationship between variables in a multivariate time series, we also want to know whether one variable can forecast or influence another variable. Granger causality is used for this type of analysis.

Although Granger Causality does NOT imply true causation, it is often used to infer "the influence". For example, if variable A granger causes variable B, but variable B does not granger cause variable A, we can assume that variable A influences variable B.

Let's understand details through the code.

Before applying granger causality, Lady H. suggests to do some data preprocessing:

• Remove highly correlated variables to minimize unnecessary calculations. If one variable can forecast another or be forecasted by it, then any highly correlated variables are likely to have similar effects.

• Ensure the multivariate time series is stationary. This was already done in previous stationary analysis step.

Here's the code Lady H. often uses to remove higher correlated columns.

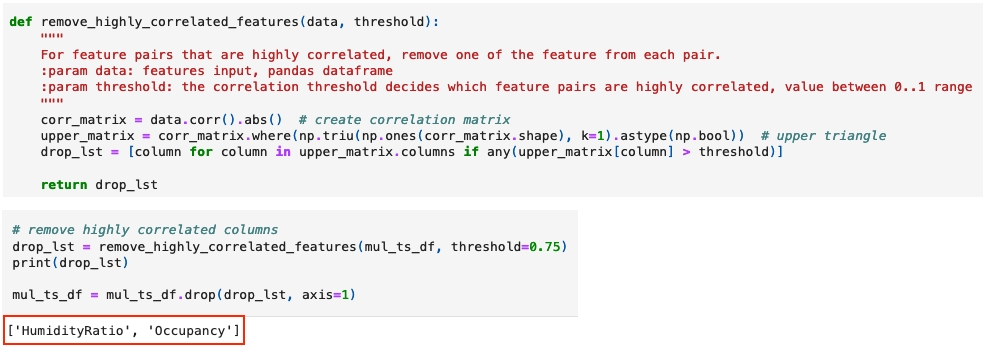
After data preprocessing, now let's look at the core logic of granger causality and the influence analysis.

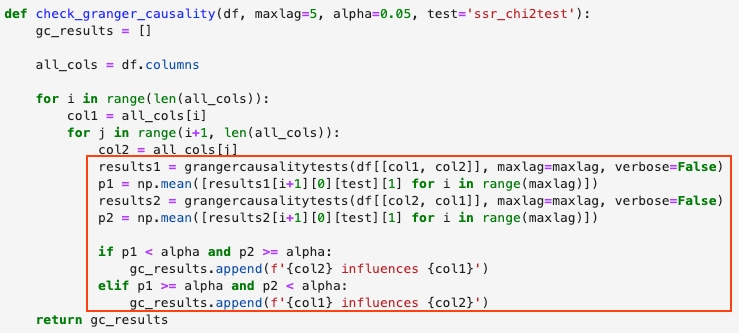
When we are using grangercausalitytests(df[[col1, col2]]), the null hypothesis and alternative hypothesis are:

• H0 (null hypothesis): col2 does not granger cause col1

• H1 (alternative hypothesis): col2 granger causes col1

Therefore when we have found col2 granger causes col1 but col1 doesn't granger cause col2, then we assume col2 can influence col1, and vice versa.

The mutual influence of our greenhouses' data is shown below. It aligns with common sense, also discloses why the icreasing of CO2 creates a vicious circle of worsening the global environment. 😰

🌻 Check detailed code for Granger Causality